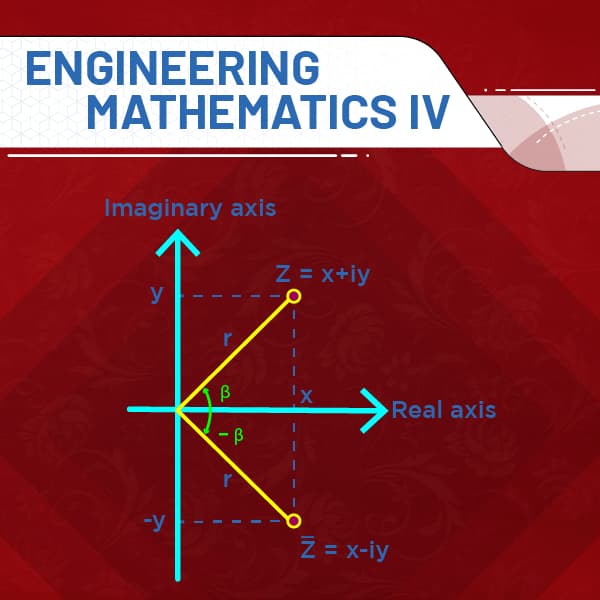
The videos herein are strictly based on syllabus of Institute of Engineering Tribhuwan University, Nepal promoting e-Learning in Nepal and are made with intention to provide guidance to the Bachelor in Engineering(BE) appearing students , for securing good results. The course tries to cover all the basics of Complex Analysis and Z-Transform. This course also comprises Partial Differential Equation and Fourier Transform with solution of most frequently asked questions in final exam of BE with fundamental theories and numericals. We strongly believe that, viewers will be benefited from these videos and the thrist of curiosity of viewers will be quenched! Feedbacks and suggestion to improve are always welcome and highly appreciated!